Geoestatistica: o que é e para que serve?
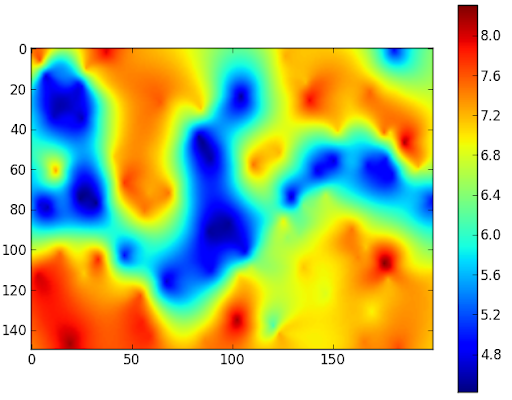
A Geoestatística possui como objetivo estudar a variabilidade espacial dos dados.
A utilização da mesma é necessária, pois quando se está trabalhando com dados geoespaciais o valor de um dado está diretamente relacionado ao valor de seus vizinhos.
Ou seja, existe dependência espacial. Dependência esta que as ferramentas da estatística clássica não consideram.
Origem da geoestatística
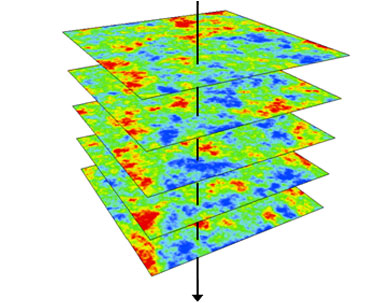
A teoria das variáveis Regionalizadas foi desenvolvida Georges Matheron, a partir de 1960.
Posteriormente, o desenvolvimento da mesma foi apoiado por diversos trabalhos de natureza empírica, realizados por pesquisadores nas minas da África do Sul, entre os quais se destacam Krige e Sichel.
Aplicações da Geoestatística
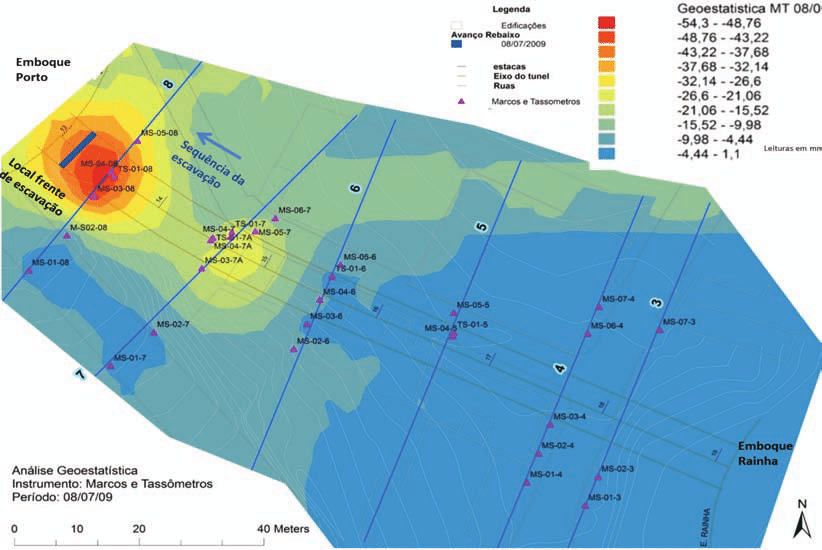
A geoestatistica se aplica a diversas áreas. Como exemplos temos:
- Agricultura de precisão;
- Estudos epidemiológicos;
- e Geologia.
Variáveis regionalizadas
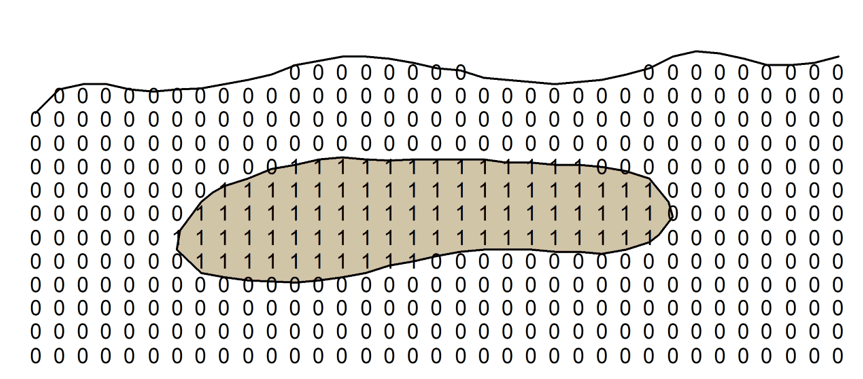
O elemento básico da Geoestatística é a variável regionalizada, cuja variação espacial caracteriza o fenômeno regionalizado que a originou.
Estas variáveis possuem características casuais e estruturadas. Ou seja, podem assumir localmente qualquer valor segundo uma função de probabilidade e globalmente, possuem uma estruturação que pode ser tratada por uma função espacial.
Geoestatística e a Interpolação espacial

A interpolação é uma técnica utilizada para a estimativa do valor de um atributo em locais não amostrados, a partir de pontos amostrados na mesma área ou região.
A interpolação espacial converte dados de observações pontuais em campos contínuos, produzindo padrões espaciais que podem ser comparados com outras entidades espaciais contínuas.
O raciocínio que está na base da interpolação é que, em média, os valores do atributo tendem a ser similares em locais mais próximos do que em locais mais afastados.
Esse conceito também fundamenta a base das relações espaciais entre fenômenos geográficos, utilizando a correlação espacial como meio de diferença dos atributos estimados.
Geoestatística – Métodos de interpolação espacial
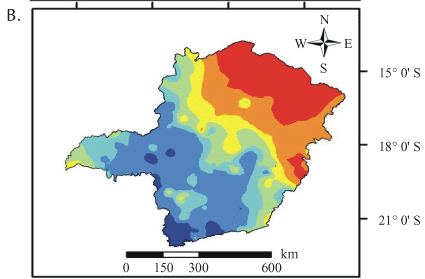
Os métodos de interpolação mais comuns dos SIGs em geral pertencem a duas categorias: globais e locais, sendo os globais mais utilizados em superfícies de tendência, e os locais podem ser polinômios de baixa ordem, funções spline, poliedros, triangulação e médias móveis ponderadas.
Porém, estes métodos não fornecem os erros associados às estimativas. Somente o método da krigagem o faz por meio de um “modelo contínuo de variação espacial”.
Ponderação do Inverso das Distâncias (IDW)
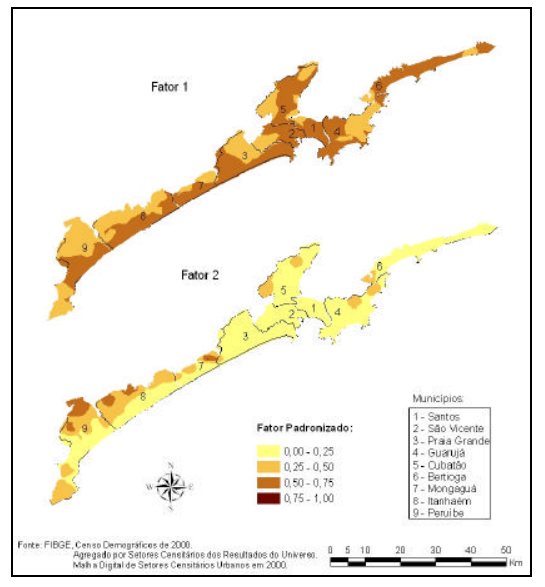
A Ponderação do Inverso das Distâncias (Inverse Distance Weighting) é um método de interpolação estatística que implementa explicitamente o pressuposto de que as coisas mais próximas entre si são mais parecidas do que as mais distantes.
Para predizer um valor para algum local não medido, o IDW usará os valores amostrados à sua volta, que terão um maior peso do que os valores mais distantes.
Ou seja, cada ponto possui uma influência no novo ponto, que diminui na medida em que a distância aumenta, daí seu nome.
Interpolação Polinomial Global
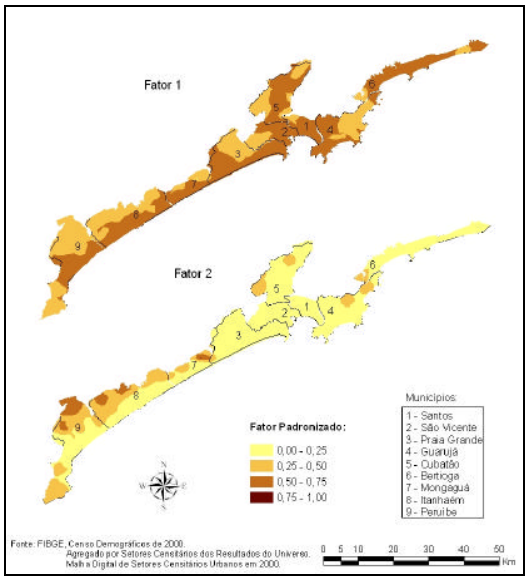
A interpolação polinomial global ajusta uma superfície suavizada definida por uma função matemática (polinomial) aos pontos observados.
Esta superfície gradualmente muda e captura o padrão de escala dos dados. Seria como ajustar um plano aos pontos observados, que pode ser linear (função polinomial de primeira ordem), de segunda ordem (quadrática), de terceira ordem (cúbica), até a décima ordem.
O resultado é uma superfície matemática suavizada, que representa as tendências graduais da superfície da área de interesse.
Interpolação Polinomial Local
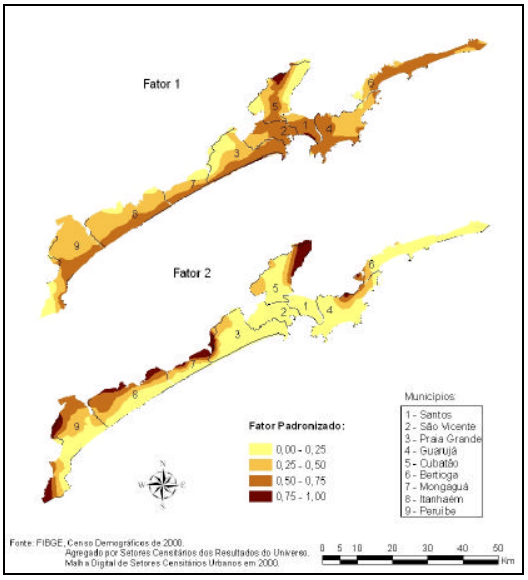
A interpolação polinomial global é um método de interpolação geoestatistica que ajusta um polinômio à superfície toda. A polinomial local pode ajustar muitos polinômios, cada um especificando sua vizinhança.
Podem ser especificados a forma, o máximo e o mínimo número de pontos a serem usados e a configuração do setor, assim como uma função de diminuição de pesos a partir da distância dos pontos, em conjunto com o poder do teste “p”.
Funções de Base Radial
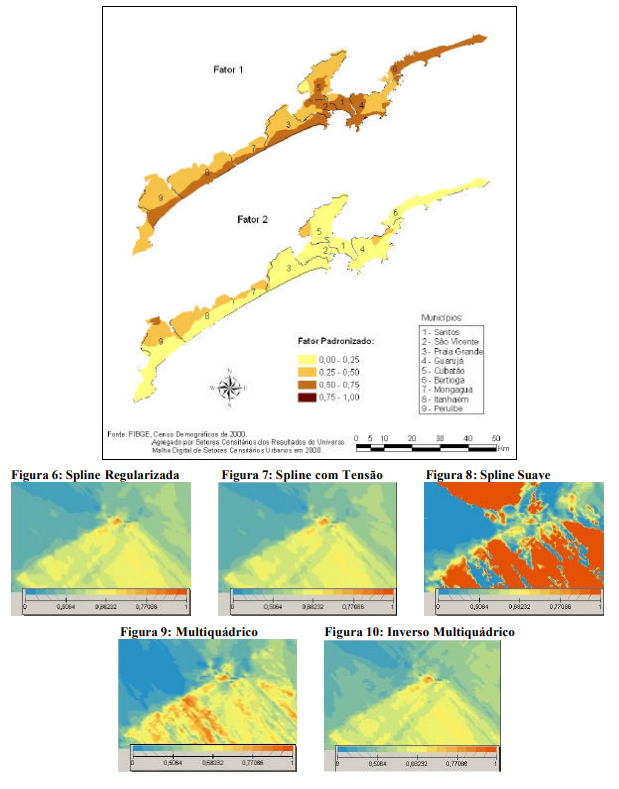
As Funções de Base Radial são interpoladores determinísticos moderadamente rápidos e exatos. São mais flexíveis que o IDW, mas exigem mais parâmetros de decisão.
Não é realizada uma avaliação da predição de erros. No entanto, fornece uma predição de superfícies que é comparável a forma exata do método de krigagem.
Este método também não permite que seja investigada a autocorrelação entre dados, sendo do mesmo modo menos flexível e mais automático que o método de krigagem.
Como nos métodos anteriores, hipóteses iniciais também não são requeridas para os dados.
Krigagem
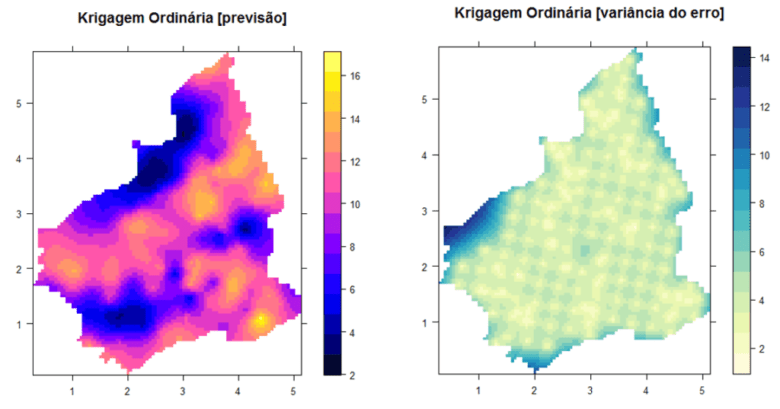
Os métodos de krigagem dependem de modelos matemáticos e estatísticos, assim como da noção de autocorrelação.
Na estatística clássica, assume-se que as observações são independentes, ou seja, não há correlação entre as observações.
Na geoestatística, a informação dos locais espaciais permite o cálculo das distâncias entre as observações e modelar a autocorrelação como uma função da distância.
A distância utilizada não é a euclidiana e sim uma distância estatística que expressa tanto a distância como a variabilidade dos dados.
A função mais comum utilizada é o (semi)variograma.
Geoestatística – Variograma
O variograma é uma ferramenta básica de suporte às técnicas de krigagem, que permite representar quantitativamente a variação de um fenômeno regionalizado no espaço.
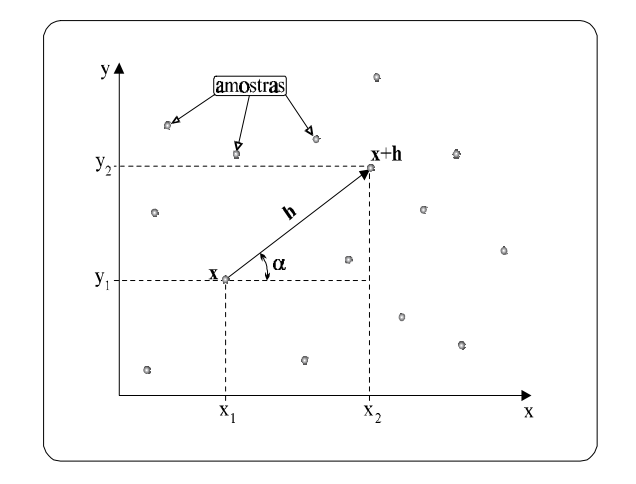
Parâmetros do Semivariograma
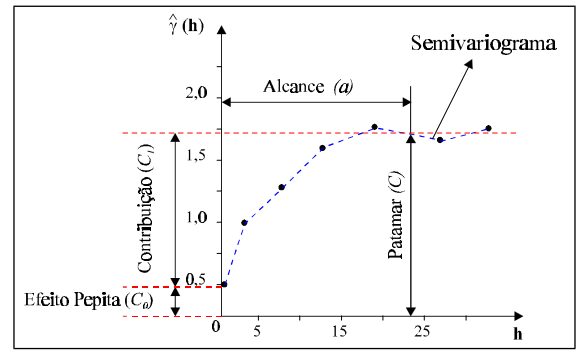
Existem 4 parâmetros que você precisa levar em consideração ao modelar o variograma. São eles:
- Alcance;
- Patamar;
- Efeito pepita e;
- Contribuição.
Alcance (a): distância dentro da qual as amostras apresentam-se correlacionadas espacialmente. Na Figura acima, o alcance ocorre próximo de
25m.
Patamar (C): é o valor do semivariograma correspondente a seu alcance (a). Deste ponto em diante, considera-se que não existe mais dependência espacial entre as amostras, porque a variância da diferença entre pares de amostras torna-se invariante com a distância.
Efeito Pepita (C0): idealmente, g(0)=0. Entretanto, na prática, à medida que h tende para 0 (zero), g(h) se aproxima de um valor positivo chamado Efeito
Pepita (C0), que revela a descontinuidade do semivariograma para distâncias menores do que a menor distância entre as amostras.
Parte desta descontinuidade pode ser também devida a erros de medição (Isaaks e Srivastava, 1989), mas é impossível quantificar se a maior contribuição provém dos erros de medição ou da variabilidade de pequena escala não captada pela amostragem.
Contribuição (C1): é a diferença entre o patamar (C) e o Efeito Pepita (Co)
Geoestatística – Tipos de krigagem
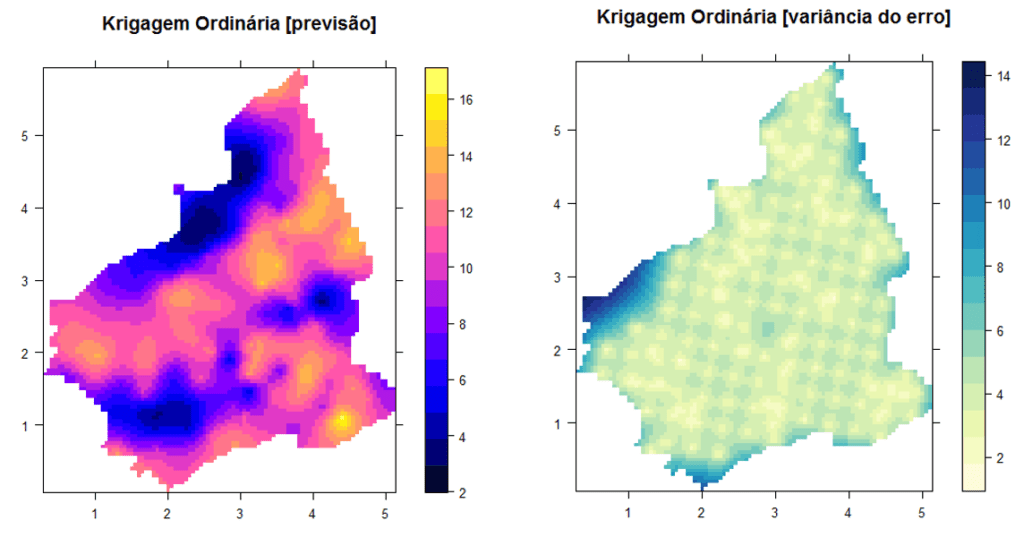
Existem diversos tipos de krigagem. As mais comuns são a krigagem simples, a ordinária, a universal, de indicadores, de probabilidade e a disjuntiva.
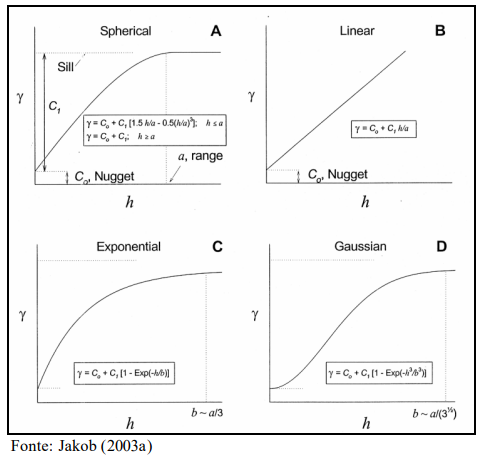
Modelos teóricos
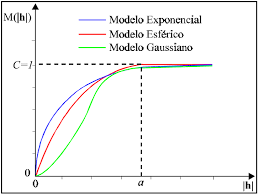
Na geoestatística o procedimento de ajuste não é direto e automático, mas sim interativo, pois nesse processo o intérprete faz um
primeiro ajuste e verifica a adequação do modelo teórico.
Dependendo do ajuste obtido, pode ou não redefinir o modelo, até obter um que seja considerado satisfatório.
Os principais modelos existentes são:
- Modelo esférico;
- Modelo Exponencial;
- Modelo Gaussiano e;
- Modelo potência.
Literatura utilizada para a escrita do artigo
Este artigo é um recorte que se baseou em 2 materiais didáticos.
“O uso de métodos de interpolação espacial de dados nas análises sociodemográficas“, de autoria de Jakob A. A. E. e Young A. F e;
“Geoestatistica: Fundamentos e Aplicações” de autoria de Eduardo Celso Gerbi Camargo.
Se você quer MERGULHAR FUNDO e aprender a prestar serviços com grande velocidade e com segurança, acesse este link e conheça os mesmos.
Entre eles, o Curso de Confecção de Plantas Topográficas. Um curso prático com o qual você vai aprender a produzir as 15 diferentes plantas produzidas em um escritório de topografia.
Clique neste link e conheça melhor o mesmo.
Gratidão por você ter lido o artigo. 🙏
Aprenda a Prestar Serviços de Topografia Através de um Livro Formado Por Mais de 547 Estudos de Caso e Exemplos Práticos

A 1 clique de distância de você encontra-se o MAIS COMPLETO LIVRO DE TOPOGRAFIA DO BRASIL.
O mesmo é formado por mais de 547 Estudos de Caso, Conhecimentos Práticos, Exemplos, Aplicações, Planilhas e Chacklists!
Se você quer (ou precisa) aprender a prestar serviços de Topografia, este livro servirá como uma luva para você.
Dê uma espiadinha no sumário do mesmo:
Para conhecer melhor a estrutura do livro, juntar-se a dezenas de profissionais e adquirir sua cópia é só clicar no botão abaixo:








