Transformada de Fourier?

Transformada de fourier, você acabou de encontrar artigo definitivo sobre o tema.
Com a leitura do mesmo você aprenderá:
- O que é a transformada de fourier;
- Quais os diferentes tipos de filtragem existentes;
- O que é a filtragem no domínio da frequência;
- Utilização da transformada de fourier;
- Os 4 tipos de filtros existentes e qual o resultado da utilização dos mesmos.
Prossiga a leitura com máxima atenção, pois o conteúdo é ouro puro.
Transformada de fourier – O que é a filtragem de imagens

Fonte da imagem: https://treinamentomaratona.wordpress.com/
Em qualquer imagem sempre é observado uma forte interdependência da vizinhança espacial dos valores dos pixels, porque os alvos na natureza tendem a mostrar uma homogeneidade dentro de certos espaços.
Essa interdependência pode ser utilizada para realçar de forma seletiva detalhes geométricos da imagem, como as bruscas mudanças ou bordas entre áreas aparentemente homogêneas, que na realidade se configuram como limites.
Mas também observamos nas imagens a presença de feições que marcam, por assim dizer, o rompimento desta interdependência, e que não parecem estar associadas a limites ou bordas de áreas, e que neste caso são identificadas como ruídos.
As técnicas de processamento que atuam no sentido de realçar as bordas ou limites e de reduzir a presença dos ruídos, são denominadas de filtragens.
Os diferentes tipos de filtragem de imagens existentes
No processamento de imagens de sensoriamento remoto, existe a filtragem no domínio espacial e a filtragem no domínio da frequência, a qual usa o conteúdo do espaço global da imagem.
No caso, neste outro artigo aqui do blog eu mostrei a filtragem no domínio espacial.
Aqui abordaremos a filtragem no domínio da frequência, onde o operador transformada de Fourier, usa o conteúdo do espaço global da imagem.
Transformada de fourier – Filtragem no domínio da frequência
Uma imagem não é composta unicamente de altas e baixas frequências. Tanto que se plotarmos em um gráfico as variações das frequências de brilhos que uma imagem pode conter, obteremos uma curva complexa do tipo mostrado na Figura abaixo.
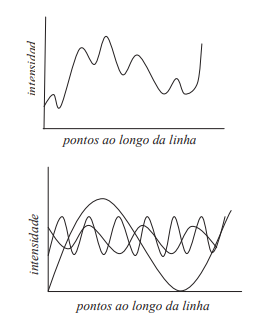
Essa curva complexa (não periódica) pode ser decomposta em vários componentes de seno e cosseno, que nos dá uma ideia da distribuição espacial de frequência da imagem.
Para decompor a imagem em seus componentes de seno e cosseno, como visto na figura acima, usa-se a Transformada de Fourier.
No domínio de Fourier cada ponto da imagem representa uma frequência única que está contida no domínio espacial da imagem.
Utilização da transformada de fourier
A utilização da transformada de Fourier se estende às várias aplicações para a reconstrução e compressão de imagens, tomografia e detecção de vozes.
Matematicamente, o entendimento da mesma é bem mais complexo do que filtrar uma imagem no domínio do espaço. Porém, a transformada Fourier torna mais fácil processar ou examinar certas frequências que influenciam na estrutura geométrica da imagem.
Como exemplo temos a presença de ruídos periódicos, que frequentemente são encontrados em quase todos os tipos de imagens de sensoriamento multiespectral.
Para o processamento de imagem digital, a qual é uma função bidimensional discreta, se utiliza da Transformada de Fourier Discreta, que é uma versão da transformada Fourier.
A transformada discreta não contém todas as frequências da imagem, mas apenas um conjunto de frequência que é suficiente para descrever completamente o domínio espacial da imagem.
Conforme é demonstrado na figura abaixo, o processo de filtragem no domínio da frequência é um processo de dois passos. Primeiro, para que os dados do domínio espacial sejam analisados no domínio da frequência necessitamos utilizar a Transformada de Fourier direta.
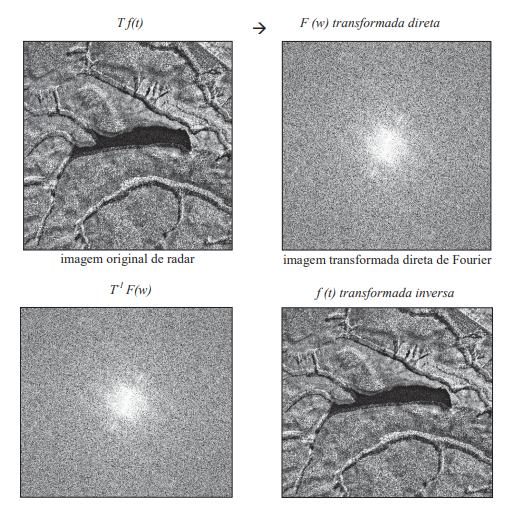
Em seguida, a Transformada de Fourier inversa é usada no sentido contrário. Ou seja, de volta ao espaço original da imagem (frequência no tempo).
O valor de brilho médio da imagem, isto é, o componente de frequência zero, é mostrado no centro da imagem transformada.
Os pixels distantes do centro representam crescentes componentes de frequência espacial da imagem. Diversas opções de filtro podem ser utilizadas para remover um componente particular de frequência da imagem.
Amostragem
Existe uma relação que descreve o compromisso entre o domínio do espaço (tempo) e o domínio da frequência, que é chamada relação de Nyquist (equação abaixo). Essa relação deve ser respeitada em função de ocorrerem efeitos denominados de aliasing.
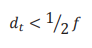
Esse limite de amostragem permite que a relação de tempo e espaço possa ser realizada sem perda de informação do sinal original.
Vamos realizar um exemplo com a imagem original que estamos utilizando de tamanho de 400 x 400 pixels amostrados para 1200 x 1200 pixels. Calculando a Transformada de Fourier das duas imagens temos os resultados na Figura abaixo.

A relação entre as operações nos dois domínios, tempo e frequência, isto é, a convolução no domínio do tempo corresponde à multiplicação no domínio da frequência.

Transformada de fourier – Os 4 tipos de filtros
Os 4 tipos de filtros definidos são:
- Filtro Passa Alta Circular;
- Filtro Passa Baixa Circular;
- Filtro Banda Passante Circular Interno e;
- Filtro Banda Passante Circular Externo.
Vamos conhecer melhor os mesmos.
Transformada de fourier – Filtro Passa Alta Circular
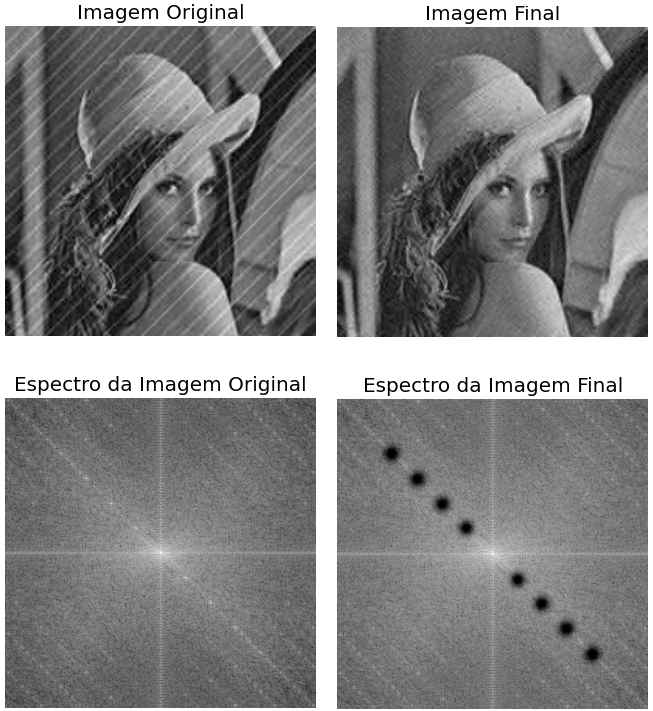
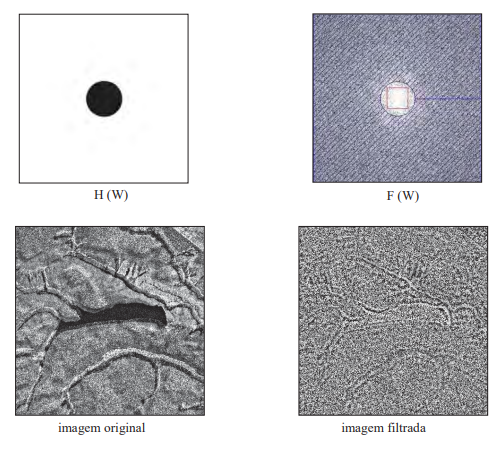
O filtro passa alta circular corta as frequências externas ao circulo (região cinza) e deixa passar as frequência internas ao circulo (região clara).
Pode-se concluir que a região clara da Transformada de Fourier está associada às altas frequências e a região cinza às baixas frequências É necessário que o analista defina alguns parâmetros, tais como o raio em pixel do círculo.
Utiliza-se esse tipo de filtro para obter as feições de detalhe na imagem (passa alta), conforme mostrado na figura abaixo:
Filtro Passa Baixa Circular
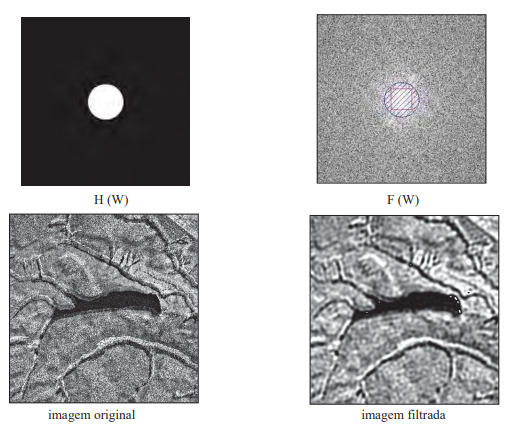
O filtro passa baixa circular corta as frequências internas ao circulo (região clara) e deixa passar as frequências externas ao circulo (região cinza). Nesse caso, utiliza-se esse filtro para obter as feições de regionais na imagem (passa baixa).
Transformada de fourier – Filtro Banda Passante Circular Interno
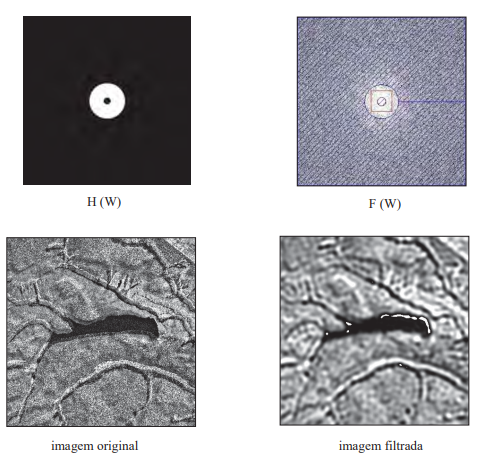
O filtro passa banda passante circular interno corta as frequências internas ao círculo menor e externas ao circulo maior (região com traços azuis) e deixa passar as frequências internas ao circulo maior e externa ao menor (região clara).
Pode-se concluir que o filtro banda passante deixa passar as frequências na região entre os círculos e corta as demais frequências. Utiliza-se esse filtro para obter as feições de detalhes limitados.
Filtro Banda Passante Circular Externo
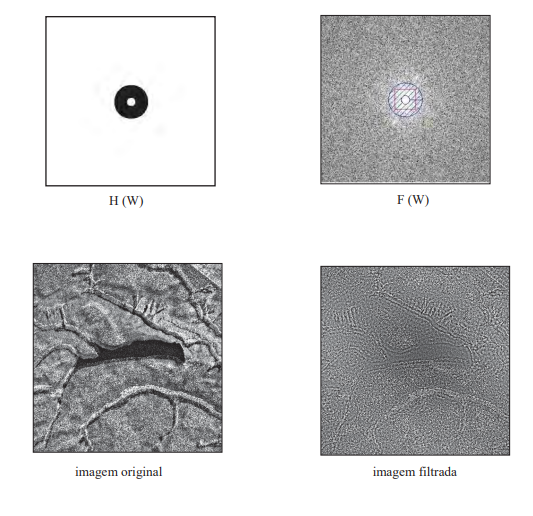
O filtro passa banda passante circular externo corta as frequências entre os dois círculos (região com traços azuis) e deixa passar as demais frequências. Pode-se concluir que as frequências entre os círculos são de frequências baixas e muito altas.
Quando utilizamos esse filtro é para obtermos as feições de maiores detalhes e regionais.
Materiais de estudos sobre filtragem de imagens
No caso, este artigo se baseou no capítulo 11 do livro “Introdução ao Processamento de Imagens de Sensoriamento Remoto“.
O mesmo pode ser baixado gratuitamente a partir deste link.
Lembrando que aqui no blog eu possuo uma uma série de artigos sobre sensoriamento remoto. Separei 2 deles para você.
> Distância de Mahalanobis: O Que É e Exemplo…
> Realce de Imagem: O Que É e Tipos Existentes…
É isso por este artigo. Gratidão por você ter lido o mesmo. 🙏
Domine a Topografia Cadastral através de um livro formado por centenas de exemplos práticos

Você quer dominar a Topografia Cadastral?
Então eu tenho uma ótima noticia para você. Me refiro ao livro Topografia Cadastral e Georreferenciamento de Imóveis Rurais na Prática.
O mesmo é dividido em 10 capítulos recheados com muitos estudos de caso e exemplos práticos. Dê uma espiadinha no sumário do mesmo:
Para conhecer melhor a estrutura do livro, juntar-se a mais de 800 profissionais e adquirir sua cópia é só clicar no botão abaixo:







